Correlation Does Not Imply Causation, So What Does?

Correlation does not imply causation is the most famous statement in the history of data analysis. It’s up there with I think, therefore I am in philosophy, E = mc2 in physics, and Hidup Jokowi in Indonesian politics. It’s easy to forget this fact and still confuse correlation with causation. Easy example: city with high number of professors also has high number of liquor stores. Does that mean number of liquor stores causes higher number of professors? I’ll let your common sense be the judge.
Why do we care about finding cause-and-effect relationships? First, this is a very natural process to us humans. We unconsciously create narratives of reasons behind why something happened. We have been doing this reasoning since we were babies. The fundamental capacity to see cause-and-effect is likely innate (or a priori), meaning it is built into our human brains. We are always craving to find cause-and-effect relationships we even do it unconsciously. Second, knowing what causes something is generally a very useful thing in life. Some examples:
- We enroll our kids to top schools for them to be successful because we think top school causes success.
- Employer creates full work from office regulation because they think work from office every day causes increase sales.
- We play classical music to our baby because we think classical music causes the baby to be smarter.
If we think otherwise, we will do the opposite action to achieve better outcome.
Correlation does not guarantee causation because of something called Bias. Bias is a "false credit". It happens when some other factor sneaks in and takes credit for the result. If we compare schools with free lunch vs no free lunch, we might see that the free-lunch schools have higher grades. But what if the free-lunch schools are just in richer areas? The "Rich" factor is boosting the grades, but the "Free Lunch" is taking the credit.
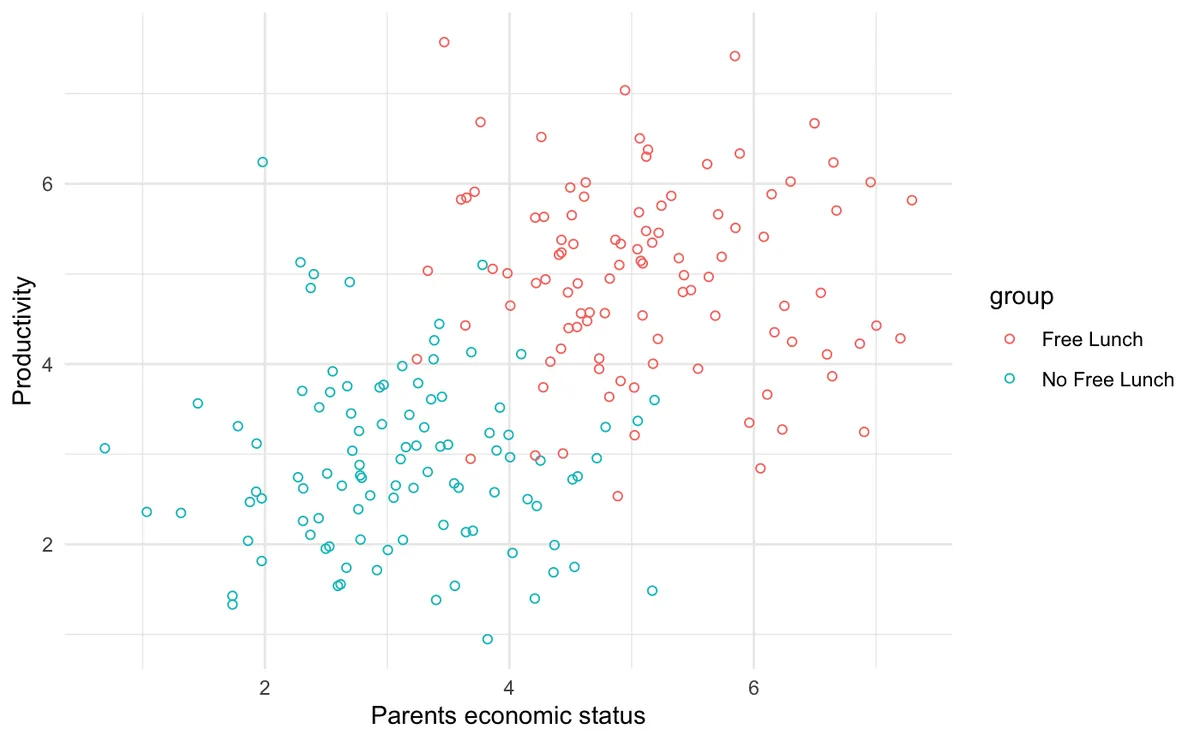
First scenario: we piloted free lunch to schools in rich area (because these schools want to contribute to the free lunch expenses). We measure the productivity after 3 months of free lunch program and we see that the average productivity for schools with free lunch is higher than schools without free lunch. The program works! Sadly this is wrong because of selection bias. Because schools with free lunch have different innate characteristics from schools without free lunch there is a lot of bias in our measurement. See the picture below for illustration.
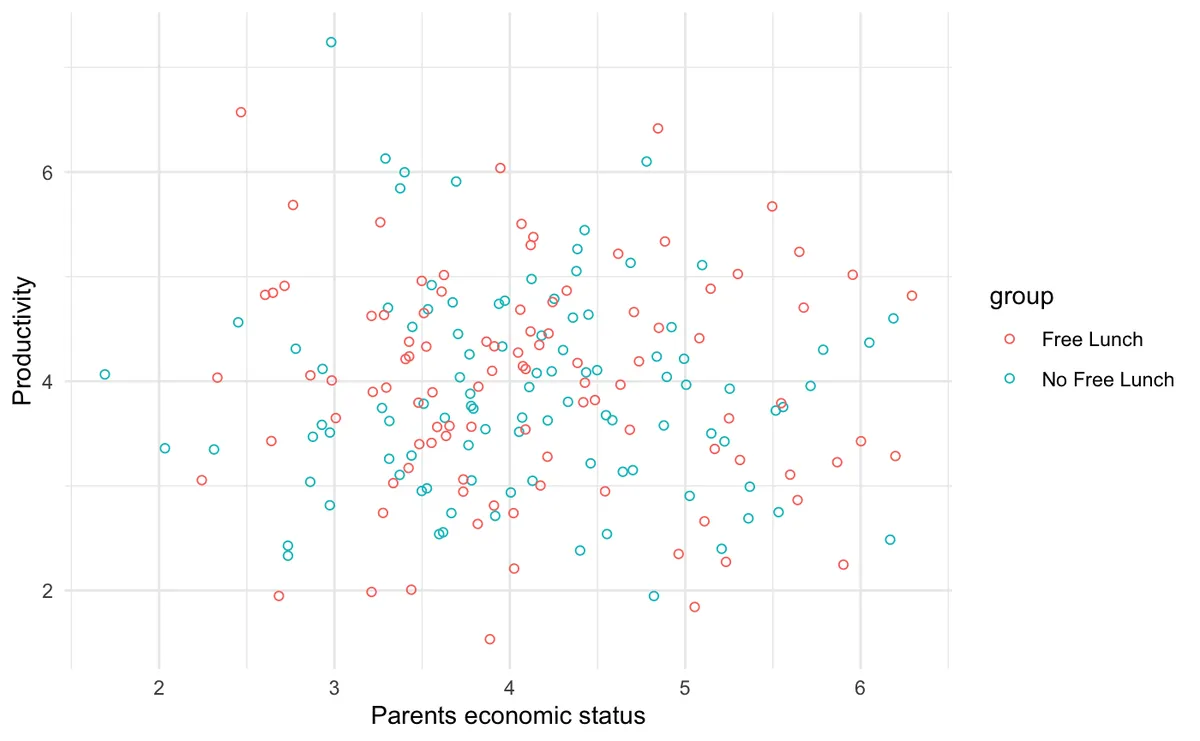
Second scenario: we piloted free lunch and randomize schools who receive free lunch and measure the productivity after 3 months of program. We see no impact on productivity caused by free lunch program. We are sure about this fact because now we remove the bias from measurement. See the picture below for illustration.
Mathematically, correlation (association) does not guarantee causation because we have non-zero bias in the correlation formula. For a more technical explanation refer to this site.
What can we do to remove bias? There are two major paths here. The most ideal one is by doing Randomized Control Trial (or A/B testing which is more popular for tech bro). Having random groups in our trial ensure there's no bias because both groups will have same characteristics. If you separate Jakarta into two big population and select people randomly you will have same proportion of billionaires, expats, sundanese, etc. in both populations.
However, you cannot always do an RCT because it takes too long, too expensive, or simply unethical. Imagine you want to know the effect of a pregnant mother smoking on her child. You cannot force 50% of pregnant mothers to smoke while letting 50% others unbothered. For this we have to do Causal Inference. For simplicity, Causal Inference uses statistical method to remove bias from the data and helps us to find causal impact of interest.